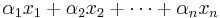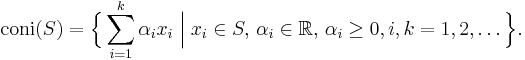Conical combination
Given a finite number of vectors 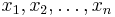 in a real vector space, a conical combination or a conical sum [1] [2] of these vectors is a vector of the form
in a real vector space, a conical combination or a conical sum [1] [2] of these vectors is a vector of the form
where the real numbers 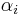 satisfy
satisfy 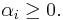
The name derives from the fact that a conical sum of vectors defines a cone (possibly in a lower dimensional subspace).
Contents |
Conical hull
The set of all conical combinations for a given set S is called the conical hull of S and denoted cone (S),[1] or coni (S)[2], that is,
By definition, the zero point (origin) belongs to all conical hulls.
The conical hull of a set S is a convex set. In fact, it is the intersection of all convex cones containing S plus the origin.[1] If S is a compact set (in particular, when it is a finite set of points), then the condition "plus the origin" is unnecessary.
If we discard the origin, we can divide all coefficients by their sum to see that a conical combination is a convex combination scaled by a positive factor.
Therefore, the "conical combination" and "conical hull" are more accurately to be called the "convex conical combination" and "convex conical hull" respectively.[1] Moreover, the above remark about dividing the coefficients while discarding the origin implies that the conical combinations and hulls may be considered as convex combinations and convex hulls in the projective space.
While the convex hull of a compact set is a compact set as well, this is not so for the conical hull: first of all, the latter one is unbounded. Moreover, it is even not necessarily a closed set: a counterexample is a sphere passing through the origin, with the conical hull being an open half-space plus the origin. However if S is a nonempty compact set which does not contain the origin, the conical hull is a closed set.[1]